集合

集合的概念

之前我们已经讲了列表和元组，他们都有着整合对象的作用。 今天的主角集合同样如此，python 中的集合与数学概念中的集合类似，就是集合中的元素不可重复。

定义一个集合

当我们建立了一个小组，组员很明显是不能重复的，这时我们就能用集合来定义。 集合的定义有两种方法，使用大括号或使用内建类型set。

group_a = {'小明', '柯南'}
group_b = set(('小新', '路飞', '小新'))
print(type(group_a))
print(type(group_b))
print(group_a)
print(group_b)

<class 'set'>
<class 'set'>
{'柯南', '小明'}
{'小新', '路飞'}

注意到打印出的结果中，顺序是被改变了的。这就是集合与列表不同的点，列表保存元素顺序而集合不会。根据集合的特性，python 帮我们自动进行了去重操作。

我们定义一个空集合时，使用的应该是set()而不是{}，因为{}代表着一个空字典（字典属于我们下一课的内容）。

obj_a = set()
obj_b = {}
print(type(obj_a))
print(type(obj_b))

<class 'set'>
<class 'dict'>

集合的操作

当我们想对集合添加元素时可以采用 add 方法， 删除元素可以使用 remove 或 discard 方法。 区别在于，remove 方法在不存在元素时会报错， 而 discard 则不然。

group = {'小明', '柯南'}
print(group)

# 往集合里添加元素
print('往集合里添加元素 add')
group.add('静香')
print(group)

# 从集合中删除元素
print('从集合中删除元素 remove')
group.remove('静香')
print(group)

# 从集合中删除元素
print('从集合中删除元素 discard')
group.discard('柯南')
print(group)

print('discard 删除一个不存在的元素')
group.discard('柯南')
print('remove 删除一个不存在的元素')
group.remove('柯南')

{'小明', '柯南'}
往集合里添加元素 add
{'小明', '静香', '柯南'}
从集合中删除元素 remove
{'小明', '柯南'}
从集合中删除元素 discard
{'小明'}
discard 删除一个不存在的元素
remove 删除一个不存在的元素
Traceback (most recent call last):
  File ".\run.py", line 22, in <module>
    group.remove('柯南')
KeyError: '柯南'

集合间的运算

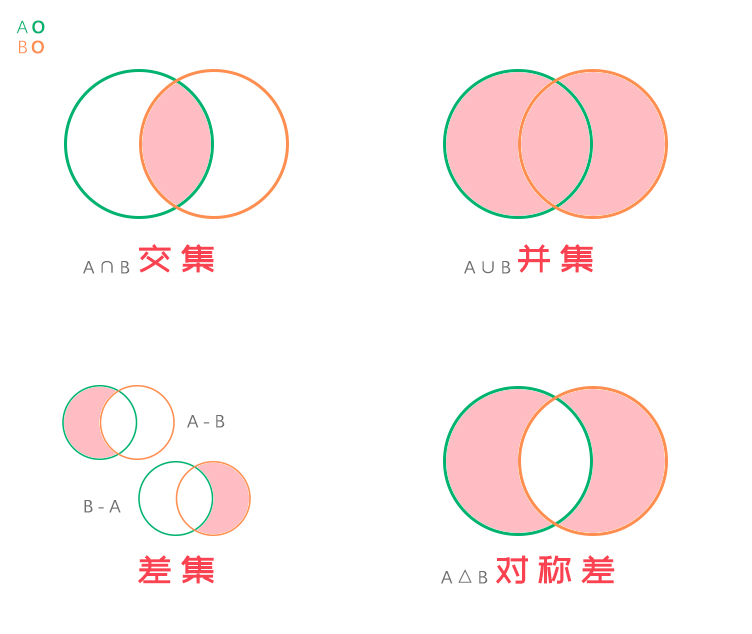
交集

求交集有两种方法，一种是直接用 & 运算符，或用 intersection 方法。

group_a = {'小明', '柯南'}
group_b = {'小明', '小芳'}
print(group_a & group_b) # group_a 和 group_b 共有的元素
print(group_a.intersection(group_b))

{'小明'}
{'小明'}

并集

求并集有两种方法，一种是直接用 | 运算符，或用 union 方法。

group_a = {'小明', '柯南'}
group_b = {'小明', '小芳'}
print(group_a | group_b)  # group_a 和 group_b 中所有的元素，去除重复项
print(group_a.union(group_b))

{'小明', '小芳', '柯南'}
{'小明', '小芳', '柯南'}

所得的并集已自动去除重复元素。

差集

差集因调用函数的对象不同返回结果也不同, 并且也是有两种方法， - 与 。

group_a = {'小明', '柯南'}
group_b = {'小明', '小芳'}
print('group_a  对 group_b 求差集')
print(group_a.difference(group_b)) # group_a 中包含而 group_b 不包含的元素
print(group_a - group_b )
print('group_b  对 group_a 求差集')
print(group_b.difference(group_a)) # group_b 中包含而 group_a 不包含的元素
print(group_b - group_a )

group_a  对 group_b 求差集
{'柯南'}
{'柯南'}
group_b  对 group_a 求差集
{'小芳'}
{'小芳'}

对称差

求对称差同样有两种方法，一种是用 ^ 运算符，或用 symmetric_difference 方法。

group_a = {'小明', '柯南'}
group_b = {'小明', '小芳'}
print(group_a ^ group_b)  # 存在于 group_a 或 group_b 中但不存在于对方中的元素
print(group_a.symmetric_difference(group_b))

{'小芳', '柯南'}
{'小芳', '柯南'}

1.存在集合 a = {1, 3, 5, 6, 7 , 8} 集合 b = {2, 4, 6, 7, 8}，运用集合运算求存在于集合 b 但不存在于集合 a 的元素。